A bit of Queuing Theory

We want to share a small study we made when trying to optimize the queue policy for a messaging system. We wanted to find an optimal configuration for a messaging system in terms of buffer size, number of threads and queue blocking policy, or at least to get a feeling of which variables come into play and which are the most affecting. Our configuration make use of the OSGi Push Stream API, for which specifications are well described. They differ from the Java Stream API because they expect data to be generated and processed asynchronously. The most important difference is that the return value of a Push Stream’s terminal operation is a Promise. This allows the Stream of asynchronously arriving data to be processed in a non-blocking way.

In order to solve our problem, the first thing we did was trying to grab some general piece of information about the topic, by simply searching through the Web. We discovered that there exists a whole theory beyond this subject, the so called Queuing Theory, which models and derives useful expressions in order to estimate the main quantities into play.

After getting a bit more familiar with the theoretical expressions, we built a simple setup which was able to plot the average system time, namely the average time our messages spent into the system, as a function of the message arrival frequency, for different configurations in terms of buffer size and processing time. Our main findings are illustrated in the figures below.

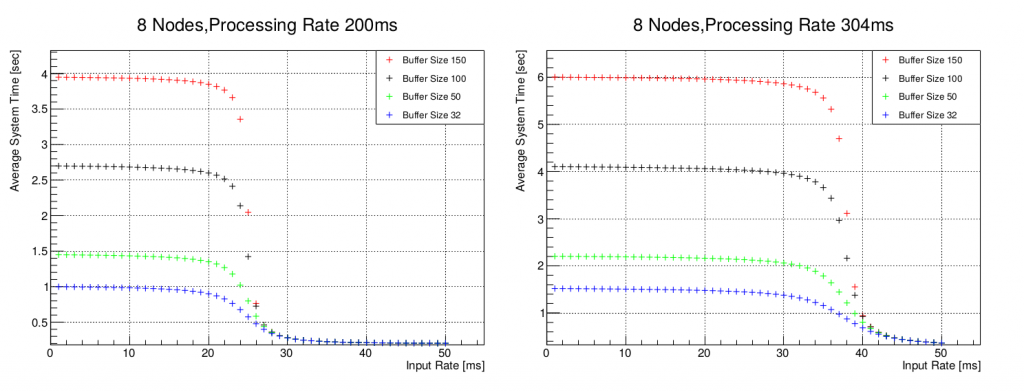Average System Time (in sec) as a function of different input times (in ms) for two fixed average processing rates of 200ms/mex (left panel) and 304ms/mex (right panel), 8 threads and different buffer sizes.

As you can see from the plots, regardless from the buffer size, which just regulates the maximum of the curve, the average system time remains quite stable for large values of the input frequency. When this reaches a certain critical value, then, we have a sudden decrease of the system time which immediately stabilizes at lower values. Looking at the same distribution for different processing rates it can be seen that the change in the curve slope depends on the ratio between the arrival and processing rate. This was a good information for us, because this means that, if we are able to predict to some extent how fast the messages are arriving and how fast we will be in processing them, we could adjust the arrival time by delaying it in such a way to reduce the system time.

Exploiting this interested result, we implemented a queue policy which, estimating the processing time for a certain message and knowing the incoming frequency, is able to apply the right delay to messages which are arriving too fast, in such a way to bring the average system time always to the right-hand side of the previous figures. We tested this new policy and compared it with a standard blocking policy by means of some JUnit tests, under different assumptions for the distributions of both the arrival time and processing time rates. For all our tests, the new policy shows a good improvement with respect to the standard blocking policy, both in terms of average time system and of the system stability.

To read more about this study and to see the detailed results, take a look at this note.

by Ilenia Salvadori, Mark Hoffmann, Jürgen Albert